 [b]
[b]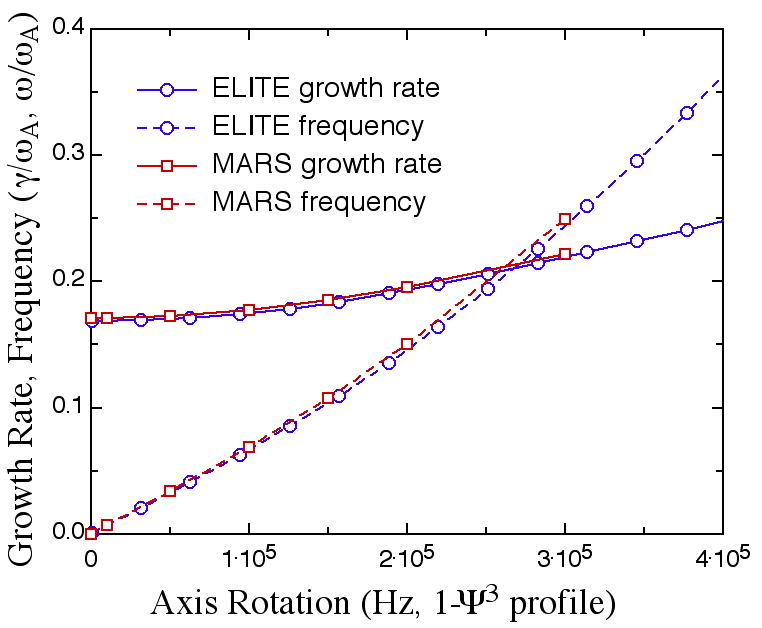

This is the home page for the ELITE edge plasma stability code, currently developed and maintained by Phil Snyder, in collaboration with Howard Wilson (University of York). The logo above shows the structure of an n=18 edge localized mode calculated by ELITE to become unstable just before an ELM is observed in DIII-D discharge 119449.
Introduction
The main aim of ELITE (Edge Localized Instabilities in Tokamak Experiments) is to perform intermediate-to-high toroidal mode number (n) MHD stability analysis of the tokamak edge transport barrier region. ELITE solves a set of 2D equations for the eigenfunction based on a rigorous expansion in inverse toroidal mode number, retaining all terms up to O(1/n) and some higher order terms to preserve the Hermitian nature of ideal MHD. The equations and definitions of variables are as reported in [1]. A brief description of the code, illustrations of its uses, and benchmarks can be found in [2,3], and further benchmarks are given below. The equations are derived using the energy principle. However, they are solved in ELITE using a general shooting algorithm, and therefore ELITE can be upgraded to include extensions beyond static ideal MHD. In its basic form, ELITE is based on incompressible, ideal MHD. However, ELITE has recently been extended to incorporate both compression and toroidal rotation. ELITE uses highly efficient numerical algorithms which allow it to be practically employed in extensive studies of large numbers of physically realistic equilibria over a wide range of n. ELITE calculates the growth rate, frequency and mode structure of n~4-200 MHD modes (typically n~4-30 is the physically relevant range for ELMs in existing tokamaks).
Code history and notes
The present non-local, intermediate to high-n version of ELITE was developed by P.B. Snyder and H.R. Wilson [1,2], building upon a previous local, high-n stability code developed by H.R. Wilson and R.L. Miller [4,5]. ELITE has been employed in scoping studies which parameterize edge stability constraints and make predictions for ITER [eg 6,7], as well as in experimental edge stability studies on a number of tokamaks including DIII-D [2,3,8-14], MAST [15], Alcator C-Mod [16], and JT-60U [17-18]. ELITE has contributed significantly to the development and validation of the peeling-ballooning model of Edge Localized Modes (ELMs) and constraints on the edge pedestal height in tokamaks. The code is written primarily in Fortran90, and has been successfully compiled on a variety of platforms, including x86 linux (with lf95, pgf90, ifc and absoft compilers), DEC alpha, and SGI Irix.
Code Verification Examples
ELITE has been successfully verified against GATO, MARS, MISHKA, DCON, CASTOR, MARG2D and BAL-MSC in a variety of cases. Two examples are given below:
[a] [b]
[b]
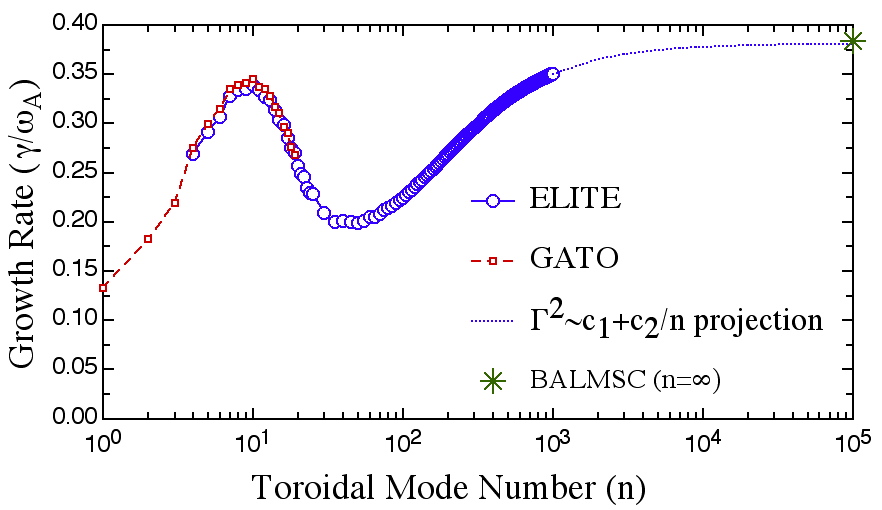
[a] Calculated growth rate vs n of an edge localized peeling-ballooning mode in a D-shaped equilibrium shows good agreement between ELITE (n=4-1000) and GATO (n=1-19) over their range of overlap (n=4-19), and shows that ELITE at high n accurately projects the n=infinity growth rate, as calculated by BAL-MSC. [b] Growth rate and mode frequency as a function of toroidal rotation frequency for a cubic rotation profile shows agreement between ELITE and MARS for this n=8 edge localized instability. This intermediate-n (n=8) mode is destabilized by a sheared toroidal flow, while higher n modes (n>~30) are stabilized.
REFERENCES
[1] H.R. Wilson, P.B. Snyder, G.T.A. Huysmans and R.L. Miller, Phys Plasmas 9 (2002) 1277.
[2] P.B. Snyder, H.R. Wilson et al., Phys. Plasmas 9 (2002) 2037.
[3] P.B. Snyder, H.R. Wilson et al., Nucl. Fusion 44 (2004) 320.
[4] J.W. Connor, R.J. Hastie, H.R. Wilson and R.L. Miller, Phys. Plasmas 5 (1998) 2687.
[5] H.R. Wilson and R.L. Miller, Phys. Plasmas 6 (1999) 1925.
[6] P.B. Snyder and H.R. Wilson, Plasma Phys. Control. Fusion 45 (2003) 1671.
[8] A.W. Leonard, T.H. Osborne et al., Phys. Plasmas 10 1765 (2003).
[9] T.W. Petrie et al., Nucl. Fusion 43 (2003) 910.
[10] P.B. Snyder, H.R Wilson, X.Q. Xu, Phys. Plasmas 12 056115 (2005).
[11] W.P. West et al, Nucl. Fusion 45 1708 (2005).
[12] K.H. Burrell et al., Phys. Plasmas 12 056121 (2005).
[13] M.R. Wade et al., Phys. Rev. Lett. 94 2250011 (2005).
[14] T. Evans et al., Nature Physics 2 414 (2006).
[15] A. Kirk et al., Plasma Phys. Control. Fusion 46 551 (2004).
[16] D.A. Mossessian, P. Snyder, A. Hubbard et al., Phys. Plasmas 10 (2003) 1720.
[17] L.L. Lao, Y. Kamada, T. Okawa, et al., Nucl. Fusion 41 (2001) 295.
[18] N. Oyama et al., Nucl. Fusion 45 871 (2005).
If you have questions on the above or would like additional information, contact Phil Snyder, extension 4088, room 13-303, email Philip.Snyder@gat.com.
This page http://fusion.gat.com/THEORY/elite/index.html was updated Monday, 4 December 2006 at 10:03:59 AM.